個別指導塾・学習塾のナビ個別指導学院

喜多方市にお住まいの皆さま、こんにちは！
喜多方市の個別塾・学習塾といえば、ナビ個別指導学院喜多方校！
教室長の金澤です。
-----------------------------------------
中学2年生のみなさん！数学の授業では『1次関数』y＝aｘ＋bを習い終わった頃だと思います！
苦手にしている生徒さんも多いため、どのように勉強すればよいかアドバイスさせていただきます！

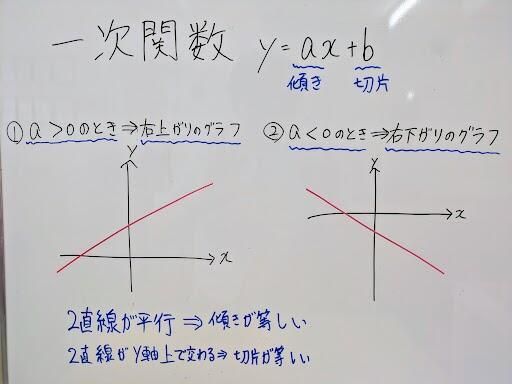
まずは、1次関数のグラフの特徴を覚えましょう。
①y=ax+bのグラフで傾きaがa＞0の時は右上がりのグラフになる。
②y=ax+bのグラフで傾きaがa＜0の時は右下がりのグラフになる。
③傾きaが等しいときは、2直線は平行になる。
④2直線の切片bが等しいときは、2直線はy軸上で交わる。

以下のような問題が出題されたときに①～④のどれを使って解けばいいかを考えてみましょう。次のア～エの１次関数について、あとの問題にあてはまるものすべてを選び、記号で答えましょう。

ア y=2x-3　イ y=-2x+6 　ウ y=-4x+6　エ y=2x+1

(1)　グラフが右上がりになるのはどれですか？
(2)　グラフが右下がりになるのはどれですか？
(3)　グラフが平行になるにはどれとどれですか？
(4)　グラフがy軸上で交わるものはどれとどれですか？

解答
(1)　「①y=ax+bのグラフで傾きaがa＞0の時は右上がりのグラフになる」を利用し、傾きaが0より大きいとき（正の数）の時は右上がりのグラフになるので、ア y=2x-3　と　エ　y=2x+1　が答えとなります。 (2)　「②y=ax+bのグラフで傾きaがa＜0の時は右下がりのグラフになる」を利用し、傾きaが0より小さいとき（負の数）の時は右下がりのグラフになるので、イ y=-2x+6 　と　ウ y=-4x+6　が答えとなります。 (3)　「③傾きaが等しいときは、2直線は平行になる」を利用し、傾きaが同じものを探し、ア y=2x-3　と　エ y=2x+1 が答えとなります。
(4)　「④2直線の切片bが等しいときは、2直線はy軸上で交わる」を利用し、切片bが同じものを探し、イ y=-2x+6　と　ウ y=-4x+6　が答えとなります。

グラフの特徴が理解できていると、複合問題が絡みやすい関数でも解きやすい問題が増えます。
まずはこの４つの問題を理解し正答できるまで勉強しましょう。

ナビ個別指導学院では最大４回の無料体験を実施しています。
もっと教えて欲しい！という方はお気軽にお問い合わせください。

【1次関数の解き方！】