南吉成の個別指導塾：式が何を表すかイメージする【高校生道場②】

仙台市にお住まいの皆さま、いつもお世話になっております！

ナビ個別指導学院　南吉成校　です！！

　

今回は２日前に書いた記事の続きです！

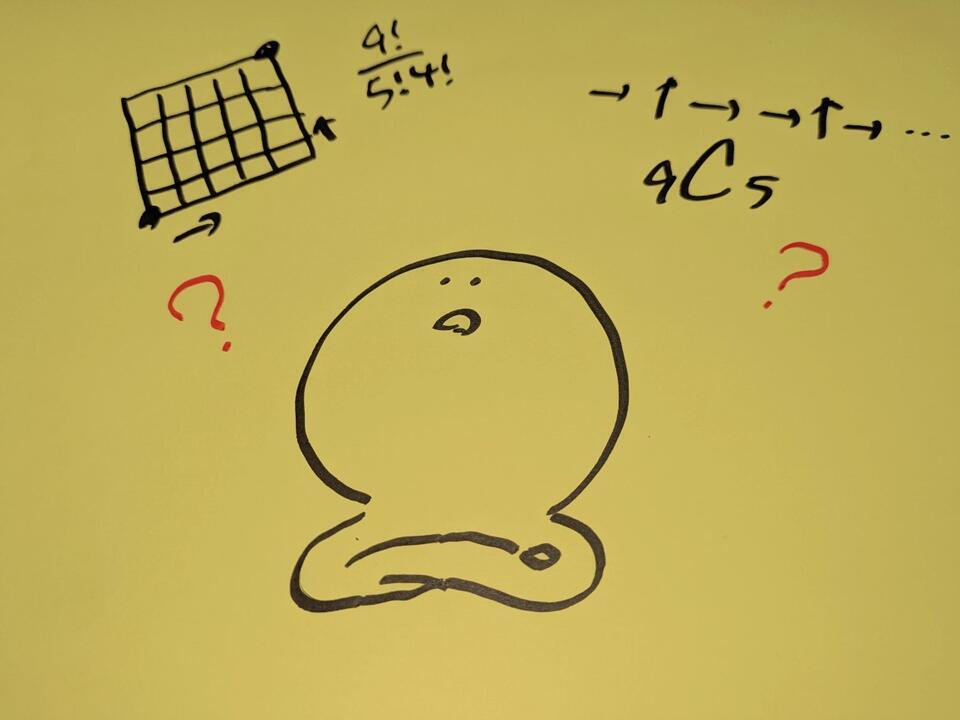
「格子状の道をAからBまで行くとき道は何通りあるか」という問題です。

ここでの考え方、式の立て方の例を２つ紹介いたします！

　

① 9! / 4! × 5! (9の階上を４の階上と５の階上の積で割る)

②９C５ (9C4 でも大丈夫です！)

　

どちらにしても　126通り　になります！

今回みなさんに注意してほしいのは、

「立てた式が、なにを表しているかをイメージ」してほしい、

ということです。　

今回の問題なら、全部で９個の道を移動しますが、(↑４回、→５回)

②の式なら、９つの箱に入れていく方法を表します。

つまり、９回の移動の内、↑の４回をどこに入れるかということです。

　

解き方は沢山ありますので、ぜひいろんな方法を模索してほしいなと

思います！　高校生の体験もこちらからお待ちしております♪

• ツイート